こんにちは。グラフィックファシリテーター®やまざきゆにこです。

野村総研　未来創発センター「データサイエンスラボ」さまの新しい取り組み　NRI「データサイエンス用語」の解説動画（絵巻物）第８弾がYouTubeアップされました。今回は（2分で解説）「秘密計算」です。

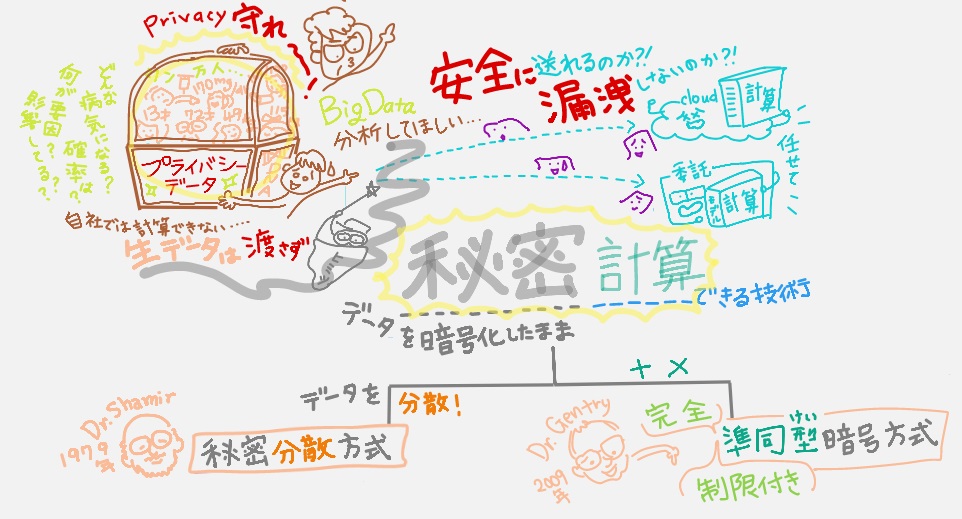
あなたのプライバシー情報を守るべく「暗号方式」が日々進化する中、今、注目されているのが今回紹介する「秘密計算」。（ゆに的に）一言で言うならば「秘密計算」＝機密データ（生データ）を「秘密に（暗号化）したまま」依頼者は委託者に渡して計算してもらえる暗号技術。

「秘密計算」詳しい用語解説はこちら。
https://www.nri.com/jp/knowledge/glossary/lst/ha/secure_computation

そもそもの話なのですが、企業は「私たちのプライバシー情報を含むデータ」を分析するとき、「社外に委託」して分析（計算）してもらうことが多々あるそうです。（①クラウドサービス事業者のサービス上でデータ分析をする　②社外の会社に委託する　という主に２つのパターンがあるそう。知らなかった…）。そこで社内の機密データ（生データ）を社外に渡して計算してもらう以上、その受け渡しの過程は常に情報漏洩のリスクと隣り合わせですね。そこで従来の「暗号方式」よりもっとプライバシー情報の保護を強化する技術として注目されてるのが今回の「秘密計算」というお話。

なんと機密データ（生データ）を「暗号化したまま」送れて、委託先も「暗号化されたデータ」のまま分析（計算）できて、その結果を返すことができるという技術！

と言われても、、、データサイエンス初心者のわたしには、そもそも従来の「暗号方式」の仕組みが分からないと「秘密計算」のすごさが分からなかったので、動画の最初は、従来の「暗号方式」の仕組みを紹介しています。

ちなみに、この従来の「暗号方式」の仕組み、「秘密鍵」と「公開鍵」という言葉が出てきて「なんだかロマンチックな世界観☆」ということで、動画では思わず「男の子から女の子に秘密の手紙を送りたい」という設定で描いてしまいました。男の子が秘密鍵と公開鍵を用意して、女の子に公開鍵だけを渡しています。男の子が秘密鍵で閉じた手紙を、公開鍵を持っている女の子だけが開けられるんです。このストーリー…素敵…デショ？？？

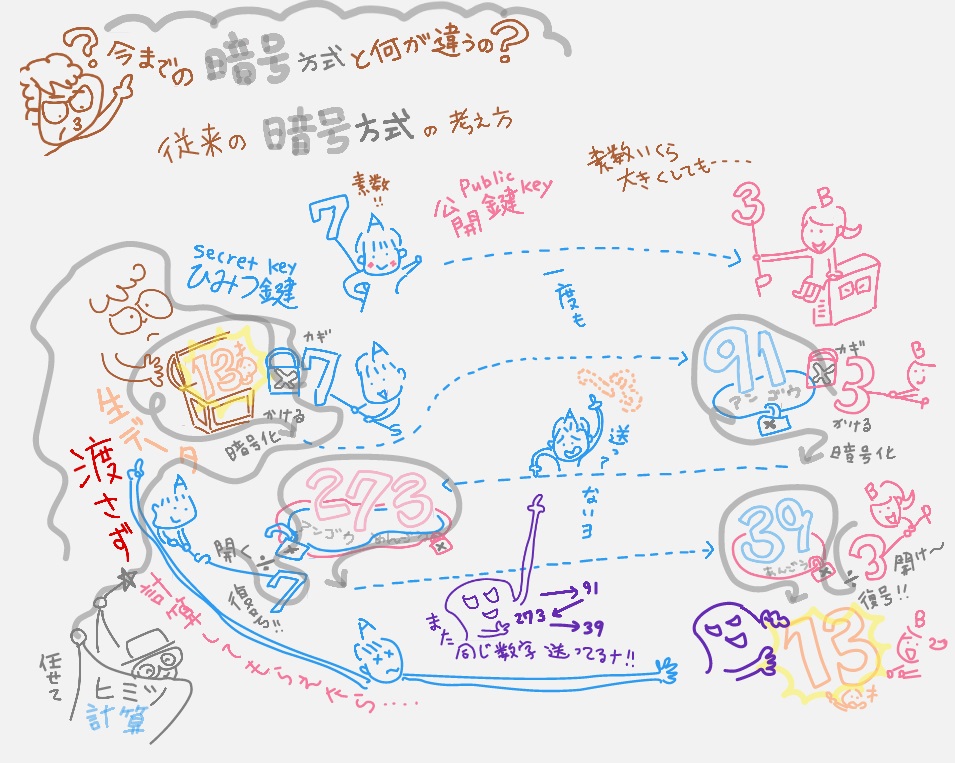
動画では、男の子が女の子だけに読んでほしい「１３」と書かれた手紙を「秘密鍵７」で閉じて女の子に「公開鍵３」を渡して開けてもらうまでの流れを紹介しています。動画は速く進んでしまうので、画像の全体像と（NRIの研究者の方に説明していただいた）解説をこちらで紹介しておきます。

①Aが公開鍵３をBに送る
②Aが秘密鍵７で１３を暗号化した９１（１３×７）をBに送る
③BがAからもらった公開鍵３で９１を暗号化した２７３をAに送る
④Aが秘密鍵７で２７３を復号化した３９をBに送る
⑤Bが公開鍵３で３９を復号化し１３を受け取る。

ちなみに、わたしは「復号」という言葉、初めて知りました(^^ゞ
「暗号」←→「復号」　

そして「掛け算・割り算」が「鍵をかける・開く」を意味しているとは！

「鍵で暗号化する」＝「鍵をかける」＝掛け算！
「鍵で復号化する」＝「鍵で開　く」＝割り算！　なんですね～

しかも鍵に使うのは「素数」とのこと。素数について語り出すと大変なことになるそうなので割愛しますが、ここでは例としてあくまでも小さい素数例で「７」と「３」を使っていますが、実際は

「ものすご～くデッカイ巨大な素数（通常は何百桁）を２つ使い、そのどちらかを秘密鍵として送り主が使う」

のだそうです。ちょっと大きな素数を例に説明してもらったも分かり易かったのでここに記載しておきます。例えば（ちょっと大きな素数の組み合わせ）「秘密鍵389×公開鍵401→155989」のように計算することは簡単だけど「155989」を389×401に素因数分解することは時間がかかる。でも「秘密鍵389」を知っている人なら155989を一瞬で割り算することができ、錠前を簡単に外せる。といった考え方です。

さて、そんな従来の「暗号方式」の弱点は主に２つ。

①女の子（委託先）の所で「復号する必要がある」のが従来の「暗号方式」。つまり、「社外の委託先（女の子）」には「１３」であると分かってしまうということ。ロマンチックな世界観で描きましたが、そもそも計算するだけが仕事の委託先にとっては、自社で漏えいする危険を冒してまで機密データ（ローデータ）の「１３」は持っていたくもないですね。

②通信上は「１３」という文字は一度も行ったり来たりしていないけれど、その行ったり来たりしている数字から結局「また同じ数字を送っているな」「きっとこのパターンで送っているのは１３だな」と見破られてしまうリスクがあるのだそう。

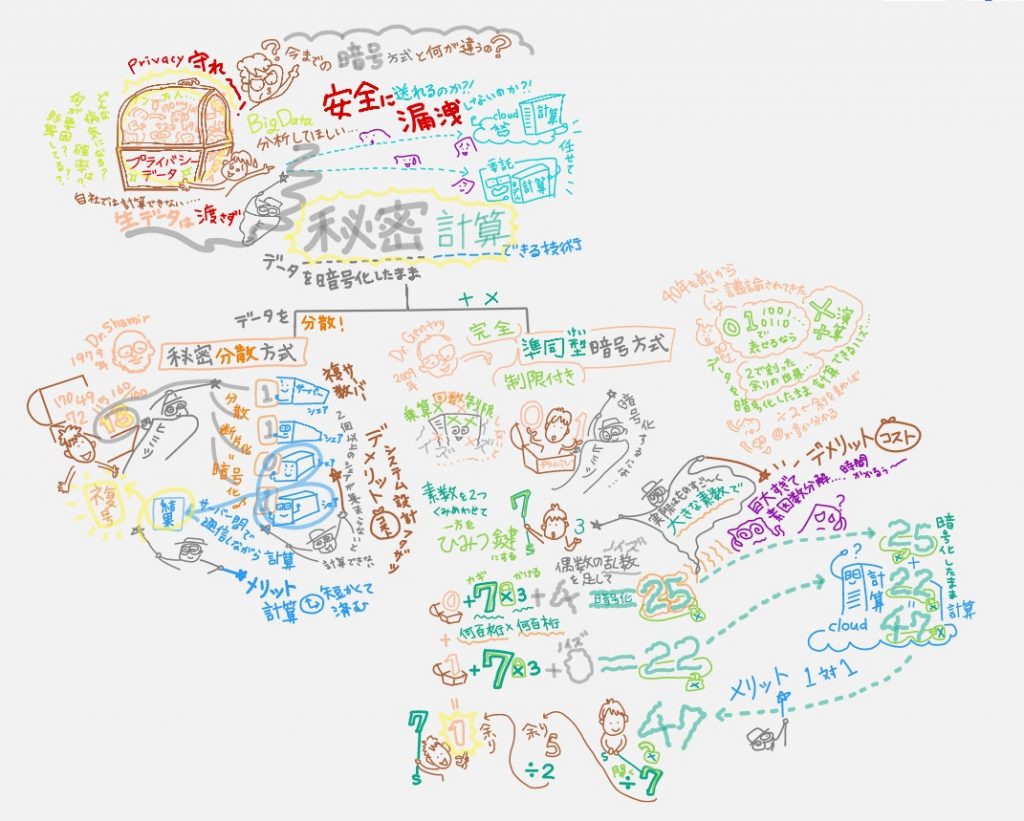
そこで、機密データ（生データ）を「暗号化したまま」送れて、委託先も「暗号化されたデータ」のまま分析（計算）できて、その結果を返すことができる技術「秘密計算」が注目されているとのこと。

暗号化されたデータを委託先は「復号する必要がない」「暗号を解かなくてもいい」んです！委託先も責任を問われなくていいですね～。委託先は暗号化されたデータのまま計算できて、その結果を返送された企業が「自ら復号する」ことで計算結果を手に入れられます。

動画では「秘密計算」の主な方式を２つ紹介しています。①データを分割する「秘密分散方式」と②演算の性質を保存する暗号関数を構成する「準同型暗号方式」。

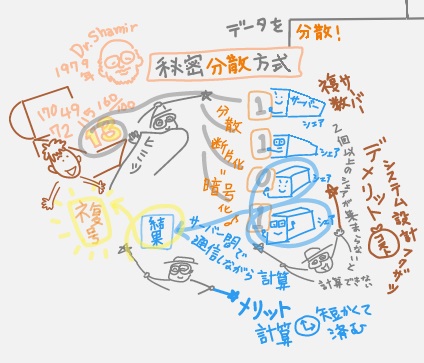
①Shamir教授が見つけた、データを分割する「秘密分散方式」

動画では機密データ（生データ）「13」を送って計算してほしいという例で描いています。「13」＝「1101」（２進法）を　分散（断片化）して４つのサーバーに計算を委託している絵です。分散している時点で、断片化＝暗号化していることになるそう。ただ一長一短あるそうで、計算は速いけど、複数のサーバーを管理するにいは設計も複雑だしコストもかかるそう。

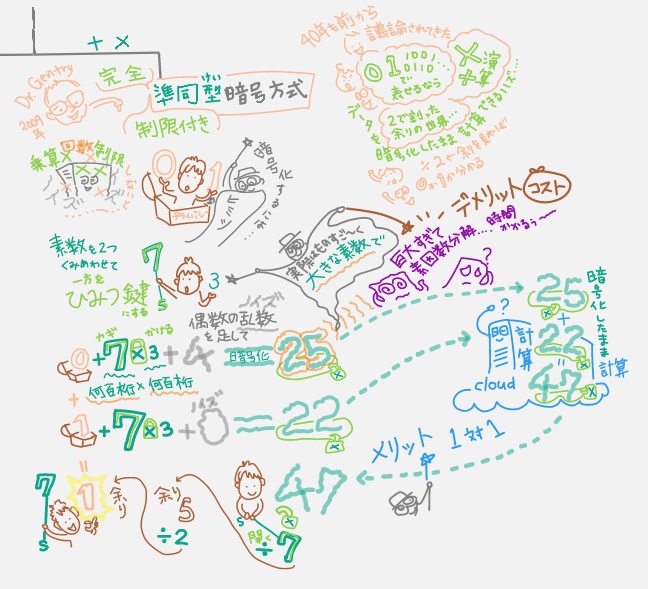
②Gentry教授が見つけた、演算の性質を保存する暗号関数を構成する「制限付き準同型暗号方式」。

「じゅんどーがた？」と読んだら「準同型（けい）です」と教えてもらいました。一般的な数学用語だそう。シロウトなわたしのざっくり理解としては

「演算（＋−×÷）を保つ」こと。これを暗号という文脈で置き換えると、「暗号化する前に演算できることは、暗号化しても演算できてその結果も同じになる」ということを言わんとしているらしい。

四則演算（＋−×÷）が行えれば「完全準同型」と言うそうなのですが、それだとデータサイズが巨大になっちゃうので「加法（＋）と乗算（×）のみ」で出来る「制限付き準同型」というのだそう。しかも「暗号方式」なので読み取られないように「ノイズ」を与えているので「乗算（×）」を重ねるとノイズが広がっちゃうとかで「乗算（×）」が制限されている、という意味でも「制限付き」なんでしょうね。

そもそも「そんなに加法（＋）と乗算（×）が大事なんですか？」ってところからわたしは引っかかっちゃったのですが「暗号がするときに適当な数字をつくれば読み取られることはないけど、復号もできない。演算ができることは大前提」なるほど、なっとく。

そしてこの暗号方式の最大のポイントが「『素数の掛け合わせ』で鍵をつくって、それに『偶数の乱数（ノイズ）を足して」暗号化している」いるから復号するとき「２で割った余りを見ればそれが０か１か分かるでしょ」という考え方なんです！そんな発想で暗号を考えていたなんて。複雑な暗号化は他にもいろいろ提案されているけれどこのシンプルさが評価されているそう。

さて、動画は速く進んでしまうので、ここでも画像の全体像と（NRIの研究者の方に説明していただいた）解説を紹介しておきます。

動画の例は機密データ（生データ）の「０」と「１」を安全に送るため、「秘密鍵７×公開鍵３」と「偶数の乱数（ノイズ）」を使って暗号化しているという絵です。「偶数の乱数（ノイズ）」＝毎回違う偶数が割り当てられるので、同じ「０」を送るときも違う暗号になるのがポイントです。ちなみに絵の中で「＝」や数字「２５」「２２」などが「ノイズでブレブレ振動している感じ」で描いてみたのですが、、、伝わってないだろうなー(^^ゞ

※実際は「素数」も「偶数の乱数」も、ものすご～くデッカイ巨大な何百桁の数字です。

↓機密データ（生データ）の「０」を安全に送るため
「秘密鍵７×公開鍵３」と「偶数の乱数（ノイズ）４」で暗号化
０＋７×３+４= ２５

↓機密データ（生データ）の「１」を安全に送るため
「秘密鍵７×公開鍵３」と「偶数の乱数（ノイズ）０」で暗号化
１＋７×３+０= ２２

暗号文を復号するとき「２で割った余りを見ればそれが０か１か分かるでしょ」がこちら。

委託先に暗号文同士で足し算してもらうと
２２＋２５＝４７

受け取った企業は計算結果「４７」を「秘密鍵７で割る（鍵を開く）」と→余りは「５」→さらに「５」を「２で割る」と→余りは「１」だから、復号結果は「１」★だと分かった。

これを念のため確認したのが下の計算。

暗号化した「２５」を「秘密鍵７で割る（鍵を開く）」と→余りは「４」→さらに「４」を「２で割る」と→余りは「０」だから←復号結果は「０」

暗号化した「２２」を「秘密鍵７で割る（鍵を開く）」と→余りは「１」→さらに「１」を「２で割る」と→余りは「１」だから←復号結果は「１」

復号結果同士の足し算０＋１＝「１」★いっしょ！間違ってない！というワケ。

現実問題、ちょっとした計算でもすごい時間がかかるそうで、まだまだ改良の余地がある段階だそうですが、数式がよく分からなくても「考え方」がシロウト的には唸っちゃうポイントですね。

改めてまとめると「制限付き準同型暗号方式」のスゴイところ。

・同じ「０」を送るにしても、送るたびに全く違う暗号で送れる。
・暗号をつくる式が
　『素数の組み合わせでつくった鍵と偶数の乱数を組み合わせてつくる』から
　暗号化したまま計算して返してもらっても
　『２で割って余りを見ればいい』シンプルなのがいい。

ふう～(*´з`)

上の画像はわたしの手書きメモのほんの一部。絵を描くなんてさいごのさいご。動画を描く前にまずもって「理解」するまでにむっちゃくちゃ時間がかかっておりまして、あたまの悪さに比例して、ウラ紙とボールペンの消費量は右肩上がりの創作現場です。

「秘密計算」詳しい用語解説はこちら。
https://www.nri.com/jp/knowledge/glossary/lst/ha/secure_computation

チャンネル登録もぜひ！
YouTube公式チャンネル　NRIデータサイエンスラボ
https://www.youtube.com/channel/UCpy_3_wYutf5u0U4DdOziGQ